-
2021 KAKAO 코딩테스트 1차 4번 풀이Python with 백준/파이썬 풀이 2022. 7. 10. 13:17
문제 4 – 합승 택시 요금
밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. “무지”는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. “무지”는 “어피치”와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을지 계산해 보고 “어피치”에게 합승을 제안해 보려고 합니다.
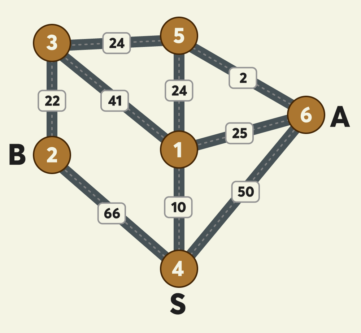
위 예시 그림은 택시가 이동 가능한 반경에 있는 6개 지점 사이의 이동 가능한 택시 노선과 예상요금을 보여주고 있습니다.
그림에서 A와 B 두 사람은 출발 지점인 4번 지점에서 출발해서 택시를 타고 귀가하려고 합니다. A의 집은 6번 지점에 있으며 B의 집은 2번 지점에 있고 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 합니다.- 그림의 원은 지점을 나타내며 원 안의 숫자는 지점 번호를 나타냅니다.
- 지점이 n개일 때, 지점 번호는 1부터 n까지 사용됩니다.
- 지점 간에 택시가 이동할 수 있는 경로를 간선이라 하며, 간선에 표시된 숫자는 두 지점 사이의 예상 택시요금을 나타냅니다.
- 간선은 편의 상 직선으로 표시되어 있습니다.
- 위 그림 예시에서, 4번 지점에서 1번 지점으로(4→1) 가거나, 1번 지점에서 4번 지점으로(1→4) 갈 때 예상 택시요금은 10원으로 동일하며 이동 방향에 따라 달라지지 않습니다.
- 예상되는 최저 택시요금은 다음과 같이 계산됩니다.
- 4→1→5 : A, B가 합승하여 택시를 이용합니다. 예상 택시요금은 10 + 24 = 34원입니다.
- 5→6 : A가 혼자 택시를 이용합니다. 예상 택시요금은 2원입니다.
- 5→3→2 : B가 혼자 택시를 이용합니다. 예상 택시요금은 24 + 22 = 46원입니다.
- A, B 모두 귀가 완료까지 예상되는 최저 택시요금은 34 + 2 + 46 = 82원입니다.
문제지점의 개수 n, 출발 지점을 나타내는 s, A의 도착지점을 나타내는 a, B의 도착지점을 나타내는 b, 지점 사이의 예상 택시요금을 나타내는 fares가 매개변수로 주어집니다. 이때, A, B 두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성해 주세요.
만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 됩니다.
제한사항- 지점 개수 n은 3 이상 200 이하인 자연수입니다.
- 지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 즉, 출발 지점, A의 도착지점, B의 도착지점은 서로 겹치지 않습니다.
- fares는 2차원 정수 배열입니다.
- fares 배열의 크기는 2 이상 n x (n-1) / 2 이하입니다.
- 예를 들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (6 x 5 / 2 = 15)
- fares 배열의 각 행은 [c, d, f] 형태입니다.
- c 지점과 d 지점 사이의 예상 택시요금이 f 원이라는 뜻입니다.
- 지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
- 요금 f는 1 이상 100,000 이하인 자연수입니다.
- fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, [c, d, f]가 있다면 [d, c, f]는 주어지지 않습니다.
- 출발 지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.
코드
 S에서 시작해서 A,B가 각각 집으로 가는 문제다
S에서 시작해서 A,B가 각각 집으로 가는 문제다
1) S에서 A,B가 같이 택시타고 가다가 도중에 내려서 각자의 길을 가거나,2) 처음부터 A,B가 따로 각자의 길을 갈 수 있다.
플로이드 워셜이라는 알고리즘을 알고 있어서 생각보다 쉬운 문제였다.
단순히 플로이드 워셜이라 알고리즘을 알고 있었고, 문제 풀어본 경험만 있어도 앞의 2,3번 문제보다 더 수월하게 해결된다.
정답은 최단경로 배열 arr[s→k] + arr[k→a] + arr[k→b] 중에서 가장 작은 값이다.** 플로이드 워셜 알고리즘모든 최단 경로를 구하는 알고리즘플로이드-워셜 알고리즘은 한 번 실행하여 모든 노드 간 최단 경로를 구할 수 있다.\
알고리즘 과정 설명

초기 그래프를 인접행렬로 나타내면 다음과 같다. INF는 해당 노드에서 특정 노드까지 가는 길이 없다는 뜻이다.
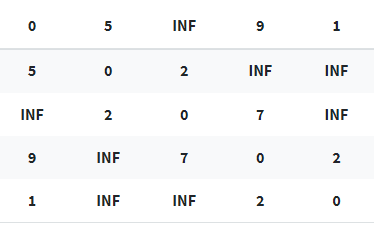
- ROUND 1 : 1번 노드를 새로운 중간 노드로 설정
이 그래프는 1번부터 5번 노드까지 존재하므로 알고리즘은 총 5라운드의 과정을 거친다. 즉, 모든 노드들을 중간 노드로 선정하는 과정을 각 라운드마다 거친다. 예를 들어 2라운드는 2번 노드가 중간 노드이며, 3라운드는 3번 노드가 중간 노드가 될 것이다.
2번에서 4번으로 가는 길은 원래 없었으나, 1번 노드를 중간 노드로 선정할 경우 2-1-4(길이 5+9=14) 로 갈 수 있게 된다. (업데이트된 길이는 📍로 표시)
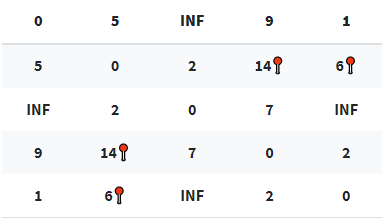
- ROUND 2 : 2번 노드를 새로운 중간 노드로 설정
1번-3번 노드를 잇는 경로, 3번-5번 노드를 잇는 경로가 새로 생기게 된다.

이런 과정으로 5번 노드를 중간 노드로 선정하는 라운드까지 모두 거치면 행렬에는 모든 노드 간 최단 거리가 들어가게 된다.
'Python with 백준 > 파이썬 풀이' 카테고리의 다른 글
백준 1727번 파이썬 문제풀이 (커플만들기) (0) 2022.07.13 백준 1726번 파이썬 문제풀이 (로봇) (0) 2022.07.11 2021 KAKAO 코딩테스트 1차 1번, 3번 풀이 (0) 2022.07.07 2021 KAKAO 코딩테스트 1차 2번 풀이 (0) 2022.07.04 2022 KAKAO 코딩테스트 1차 1번 풀이 (0) 2022.07.01